STLによる時系列データの分解について基礎から理解する

時系列分析において、時系列データをトレンド成分、季節成分、残差に分解するSTLという手法について解説します。
時系列データにおける季節成分について
時系列データには 季節成分 という厄介な成分が潜んでいる場合があります。
時系列データの季節成分とはその名の通り季節=時間に依存して周期的に変化する成分です。
例えば、日本で最高気温を1日毎に記録した時系列データを考えます。
この気温データはおおよそ夏に大きいな値を、冬に小さな値をとり、春夏秋冬に応じて周期的に変化すると考えられます。
このように 季節に応じて決まったパターンで周期的に変動する成分 を季節成分と呼びます。
多くの場合で季節成分は分析から取り除きたい対象となります。
先の気温データの例で、本当は地球温暖化の影響で徐々に気温が大きくなっていることを調べたいとします。
この場合、季節ごとの気温の変動は本当に調べたいものではなく、本来調べたいのはそのような変動を除いてもなお長期的に気温が上昇傾向にあるかどうか、です。
(本当にこのデータで地球温暖化のような現象を調べられるかは置いておいて…)
そのため 元のデータから季節成分を除いて分析をしたい という動機が考えられるわけです。
このような周期性の影響を除く簡便な方法として、前年同期比を取る という方法あります。
例えば月次の売上データに年の周期性がある場合、前年の同じ月と比較してどれほど売上が伸びたかを測れば周期性を取り除くことが可能です。
ただ、この方法だと比較可能な整ったデータが必ず2年以上分必要です。
また、周期性自身に興味があるという場合もあります。
この場合には前年同期比を取ることで周期性が取り除かれてしまっているので、周期性自身についての分析は難しいでしょう。
そのため、 時系列データそのものから季節成分を推定してそのほかの成分から分離する 、という方法が必要となります。
時系列データの分解について
時系列データから季節成分を推定する際、よく以下のように時系列データが構成されると仮定します。
$$ O_t = T_t + S_t + I_t \tag{1} $$
各々の記号の意味は以下です。
| 記号 | 意味 |
|---|---|
| \(O_t\) | 原系列(元々の時系列データ) |
| \(T_t\) | トレンド成分(以下で少し補足します) |
| \(S_t\) | 季節成分 |
| \(I_t\) | 残差(原系列からトレンド成分と季節成分を除いた残り) |
このように仮定することで、季節成分の推定が 原系列 \(O_t\) から季節成分 \(S_t\) を推定する という問題に帰着しました。
補足1: トレンド成分について
上記のトレンド成分 \(T_t\) とは時間に依存した長期的な傾向を表します。
例えば、先に例に出した地球温暖化の例では、気温が時間が経つにつれ右肩上がりに上昇しているといった状態を表します。
(これは検証されるべき問いではあります。)
経済時系列では、季節成分を1年を周期とする周期的変動として定義し、1年よりも長い周期を持つ変動を 循環成分 と呼ぶこともあります。
その場合、時系列データは(1)のトレンド成分をさらに分解して、
$$ O_t = T_t + C_t + S_t + I_t $$
と循環成分 \(C_T\) も含めて分解します。
循環成分は長期的な景気の循環を検証する際に用いられる概念ですが、本記事では扱いません。
補足2: 分解の妥当性について
そもそもこのような分解が本当に成り立っているのでしょうか?
これについては 「ここではそのような仮定を置いている」 と思っていた方が良いと考えています。
つまり、 とりあえずこのように分解されると仮定して分析を進めていく、ということです。
分析結果を原系列への当てはまり、残差の診断、人による解釈など様々な観点から検証して納得のいく結果であればその後の活用に進む、という流れが良いのではないでしょうか。
(そのためにはどのように活用していくのかを事前に決めておく必要がありますが)
考えようと思えば、さらに複雑な分解をすることは可能です。
結果を見て満足いかなければ別の分解を試してみるので良いのではないでしょうか。
ただし、ほとんどの時系列分析は(1)のような分解を前提としています。
そのため、より複雑な分解をする場合はかなり基礎的な部分からアルゴリズム考案+コード実装をする必要があるでしょう。
ただし、特殊な場合として全成分が掛け算の形で分解される場合は以下のように対数を取ることで(1)と同じ分解に帰着できます。
以下では自然対数を取っていますが対数の底は何でもかまいません。
$$ \begin{align} O_t &= T_t \times S_t \times I_t \\ \iff \ln O_t &= \ln (T_t \times S_t \times I_t) \\ &= \ln T_t + \ln S_t + \ln I_t \end{align} $$
よって原系列の対数を取ることで各成分の対数の和へと分解できるわけです。
このような積として分解されるという仮定は注目する数値が比率である場合に用いられます。
例えば経済時系列のGDP前期比などですね。
STLによる季節成分の分解
(1)式のように時系列データを分解する手法の一つとして STL(Seasonal and Trend decomposition using LOESS) があります。
詳細は説明は後述しますが、STLは簡単に言うと局所的な回帰モデル(LOESS)を用いて原系列をトレンド成分と季節成分に分解します。
R. B. Cleveland, W. S. Cleveland, J.E. McRae, and I. Terpenning (1990) STL: A Seasonal-Trend Decomposition Procedure Based on LOESS. Journal of Official Statistics, 6, 3-73.
アルゴリズムの詳細に入り込む前に、まずは実際に手元で動かしてみてSTLがどのようなアウトプットをするのか確認してみましょう。
以下のコードでサンプルデータを作成します。
サンプルデータでは日次データを想定し、日が経つにつれて単調に増加していくトレンド成分と、7日周期の季節成分、以下の式に従うノイズ成分(残差)で構成されます。
$$ I_t = 0.8 I_{t-1} + W $$
ここで \(W\) はホワイトノイズです。
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from datetime import datetime, timedelta
sns.set()
plt.rc("figure", figsize=(10, 8))
plt.rc("font", size=13)
# データ長
n = 90
# ダミーの日付列を作成
dummy_dates = [datetime(2023, 1, 1) + timedelta(days=i) for i in range(n)]
# ダミーのトレンド系列を作成
dummy_trend = 0.1 * np.arange(1, n+1)
# ダミーの季節成分系列を7日周期で作成
dummy_seasonal = 0.6 * np.sin(np.arange(n) * 2 * np.pi / 7)
# ダミーの不規則項を生成
## 不規則項 I(t) = 0.8I(t-1) + ホワイトノイズ
_wn = np.random.rand(n)
dummy_resid = np.array([0.8*_wn[t-1] + _wn[t] if t>0 else _wn[0] for t in range(n)])
# ダミーデータを合成
dummy_data = dummy_trend + dummy_seasonal + dummy_resid
# ダミーデータをデータフレームにまとめる
dummy_df = pd.DataFrame({
"date": dummy_dates,
"data": dummy_data
})
# 日付列をindexに設定
dummy_df.set_index("date", inplace=True)
display(dummy_df.head())
出力
| date | data |
|---|---|
| 2023-01-01 | 0.484005 |
| 2023-01-02 | 1.224587 |
| 2023-01-03 | 1.337571 |
| 2023-01-04 | 0.899302 |
| 2023-01-05 | 0.676021 |
サンプルデータをグラフでプロットしてみます。
sns.lineplot(x="date", y="data", data=dummy_df)
plt.xlabel("Date")
plt.ylabel("Value")
plt.xticks(rotation=45)
plt.show()
出力
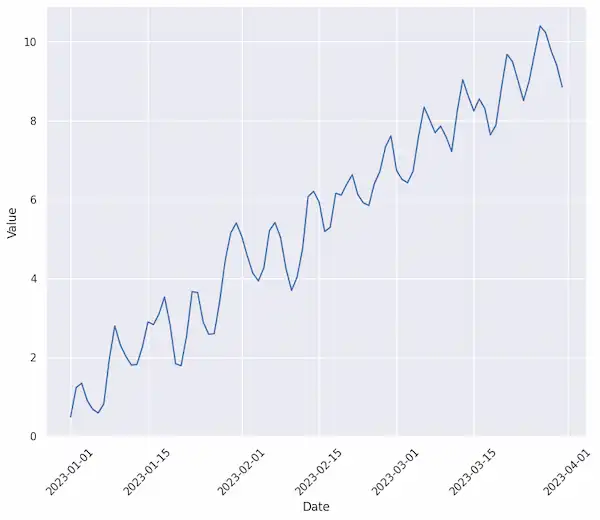
周期的に変動しつつ、右肩上がりの時系列データを作成できました。
では、このデータにSTLを適用してみます。
STLは様々な時系列分析用のライブラリから提供されていますが、ここでは statsmodels による実装を使います。
from statsmodels.tsa.seasonal import STL
# STL分解
stl = STL(dummy_df["data"], seasonal=7)
decomp = stl.fit()
# 分解の結果を図示
res = decomp.plot()
出力
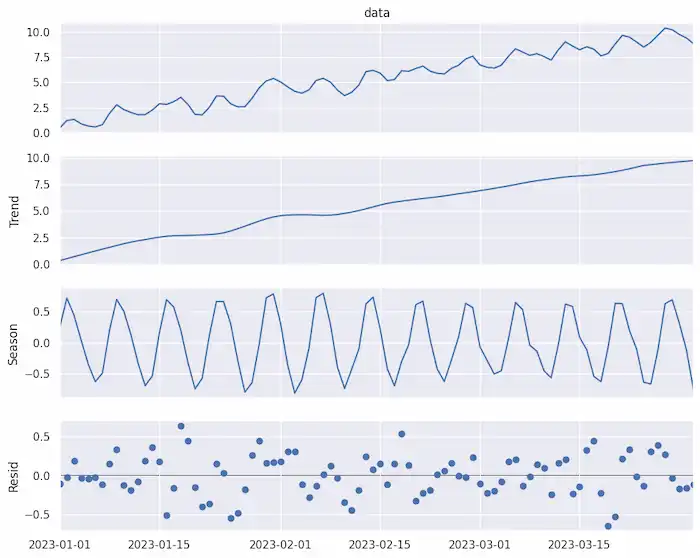
上から順に原系列、分解されたトレンド成分、季節成分、残差のプロットとなっています。2023-01-01 から 2023-01-15 の2週間でおよそ2つ分の波が出来ているので、サンプルデータで指定した1週間単位の季節成分がきちんと推定出来ていると思われます。
ただ、縦軸の範囲を見るにこのデータはほとんどがトレンド成分によって説明されることも分かります。
STLの主要な引数について説明します。
全引数のリストは 公式のドキュメント を参照していただくとして、ここでは主要な引数に絞って説明します。
endog: 分解対象となる原データ(1次元の配列)period: 原系列の日付や時間が持つ代表的な周期を正の整数で指定(月次データなら12=1年、日次データなら7=1週間)endogがpd.Seriesかpd.DataFrameの場合はindexから推定されるendogがndarrayなどindexがない配列の場合は指定が必要
seasonal: 季節成分の周期を 正の奇数 で指定- デフォルト値7
rubust: LOWESS(重みづけしたLOESS)を用いるか否かのbool値- 外れ値に対してロバストになることが期待される
以上でSTLの説明を終わります。
STLは時系列分析の前処理として簡易ながら強力な手法だと思います。
時系列データの最初の一歩(の一つ)として頭に入れておこうと思います。